top of page

Практическая работа №I.8.2

Решение тригонометрических

уравнений и неравенств

Теоретическая часть

1.PNG
1.PNG
1.PNG
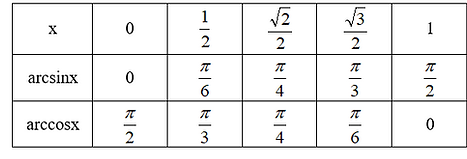
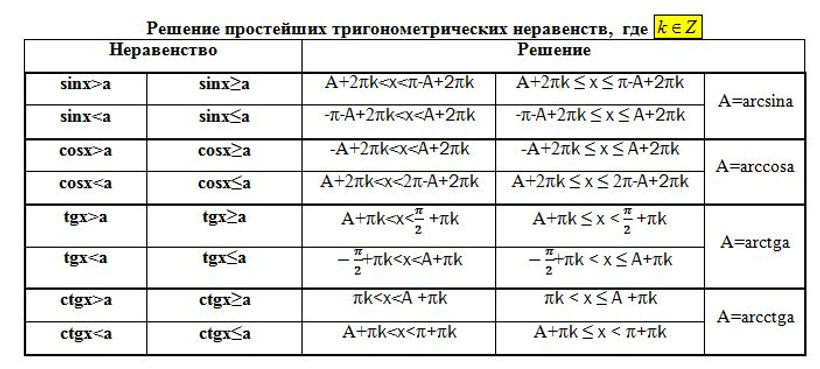
Решение однородных уравнений

Способ решения однородных уравнений второй степени:

Вид однородных  уравнений:

1.JPG

Отличительные признаки однородных уравнений:

а) все одночлены имеют одинаковую степень,

б) свободный член равен нулю,

в) в уравнении присутствуют степени с двумя различными основаниями.

Однородные уравнения решаются по сходному алгоритму.

Чтобы решить уравнение такого типа, разделим обе части уравнения на  (g(x))^2 (можно разделить на f(x)g(x)  или на (f(x))^2)

​

Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.

Если является, то мы выписываем этот корень, чтобы потом про него не забыть, а затем делим на это выражение.

​

Вообще, первым делом, при решении любого уравнения, в правой части которого стоит ноль, нужно попытаться разложить левую часть уравнения на множители любым доступным способом. А затем каждый множитель приравнять к нулю. В этом случае мы точно не потеряем корни.

​

Итак, осторожно разделим  левую часть уравнения на выражение  почленно. Получим:

2.JPG

Сократим числитель и знаменатель второй и третьей дроби:

3.JPG

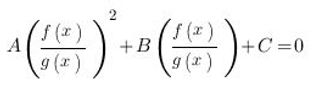
Введем замену:

t=f(x)/g(x)

,

Получим квадратное уравнение: At^2+Bt+c=0

​

Решим квадратное уравнение, найдем значения t,  а затем вернемся к исходному неизвестному.

При решении  однородных тригонометрических уравнений, нужно помнить несколько важных вещей:

1. Свободный член можно преобразовать к квадрату синуса и косинуса с помощью основного тригонометрического тождества:

4.JPG

2. Синус и косинус двойного аргумента являются одночленами второй степени -  синус двойного аргумента легко преобразовать к произведению синуса и косинуса, а косинус двойного аргумента - к квадрату синуса или косинуса:

5.JPG
bottom of page